Công cụ Tối ưu Lò xo Xoắn Ốc Spiral Torsion Spring Optimizer v3

Nhanh tay thả tym nếu thấy công cụ này hay ho nha. Nếu có dùng để làm gì rồi thì nhớ cho mình xin đánh giá và để lại comment cho mình biết bạn đã dùng nó để làm gì nha, mình rất thích xem mọi người làm gì với nó! Nếu có bất kỳ câu hỏi nào cứ để lại comment mình sẽ giải đáp sớm nhất có thể nha.

Các phiên bản tương lai của dự án này sẽ dưới dạng macro FreeCAD thay vì bảng tính Libreoffice. Các bạn có thể xem tiến độ của mình trên repository trên GitHub (mới chỉ ở giai đoạn đầu nha).

Giới thiệu:

Dự án này bao gồm một bảng tính Libreoffice Calc để tạo ra các lò xo xoắn xoắn ốc được tối ưu hóa bằng cách sử dụng tối ưu hóa nhận thức xã hội và một tệp FreeCAD tham số lấy các số liệu sao chép từ bảng tính để tạo ra mô hình 3D của lò xo được tối ưu hóa. Bằng cách tạo tệp CAD tham số của riêng bạn, bạn cũng có thể sử dụng bảng tính này để tối ưu hóa lò xo trong bất kỳ phần mềm CAD nào bạn chọn. Bảng tính cũng cung cấp một số biểu đồ hữu ích để trực quan hóa các đặc tính và hiệu quả của lò xo.

Để sử dụng công cụ này, bạn cần xác định mô đun Young và ứng suất chảy của vật liệu bạn đang in. Một số số liệu sơ bộ nhưng hữu dụng có thể tìm thấy trong bảng dữ liệu kỹ thuật được xuất bản bởi các thương hiệu filament uy tín như Prusament và Polymaker, mặc dù chúng không tính đến các yếu tố như tốc độ in, nhiệt độ in và đường kính vòi phun cũng ảnh hưởng đến các đặc tính này. Đây là một số lời khuyên về việc xác định các tham số này:

Mô đun Young (E):

Mô đun Young là thước đo độ đàn hồi của vật liệu, hay nói cách khác, vật liệu bị uốn cong hoặc biến dạng bao nhiêu khi có một lượng áp lực nhất định tác dụng lên nó. Trong bảng dữ liệu của Prusament, nó được gọi là “flexural modulus”, và trong Polymaker, nó được gọi là “bending modulus”. Polymaker cũng liệt kê một đặc tính riêng được gọi đơn giản là “Young's modulus”, nhưng đây thực chất là mô đun kéo như được liệt kê trong bảng dữ liệu của Prusament hoặc mô đun nén. Chúng ta muốn sử dụng mô đun uốn cong hoặc mô đun uốn vì chúng là sự kết hợp của mô đun kéo (kéo căng) và mô đun nén, đây là những gì thực sự xảy ra trong một lò xo xoắn xoắn ốc. Nếu bạn muốn tạo ra các lò xo lưu trữ một lượng năng lượng cụ thể một cách chính xác, hãy làm theo các bước sau để tìm mô đun Young thực tế cho vật liệu cụ thể của bạn được in trên máy in cụ thể của bạn:

1. Thiết kế một lò xo có hằng số lò xo (K) siêu cao. Điều này để đảm bảo bạn nhận được kết quả mô-men xoắn mạnh và giảm thiểu các nguồn lỗi như ma sát. Tôi đã sử dụng hằng số lò xo là 1.000 N mm/rad. Tôi đặt chiều cao là 10mm và độ dày là 8mm. Nếu bạn sử dụng của tôi, bạn sẽ cần đặt bán kính miếng đệm trung tâm (r_C) thành 10mm.
2. In lò xo bằng cài đặt tốc độ và nhiệt độ in mà bạn đã chọn khi xác định mô đun Young ban đầu. Ví dụ, tôi bắt đầu với mô đun Young là 2600 MPa, tương ứng với tốc độ in 40mm/giây và nhiệt độ 200C (đối với PLA) trong bài báo đầu tiên được trích dẫn trong thư mục. Tôi cũng thích tăng số lượng lớp vỏ dọc cho đến khi toàn bộ độ dày của lò xo được lấp đầy bằng các lớp vỏ (không có vật liệu độn). Bằng cách này, toàn bộ lò xo có các sợi nhựa đồng nhất chạy theo đường cong của lò xo thay vì các đường kẻ vật liệu độn lởm chởm.
3. Kiểm tra mô-men xoắn của lò xo ở một lượng xoắn cụ thể. Nếu bạn đang sử dụng Rad Tester của tôi, đây sẽ là một radian (do đó có tên gọi).
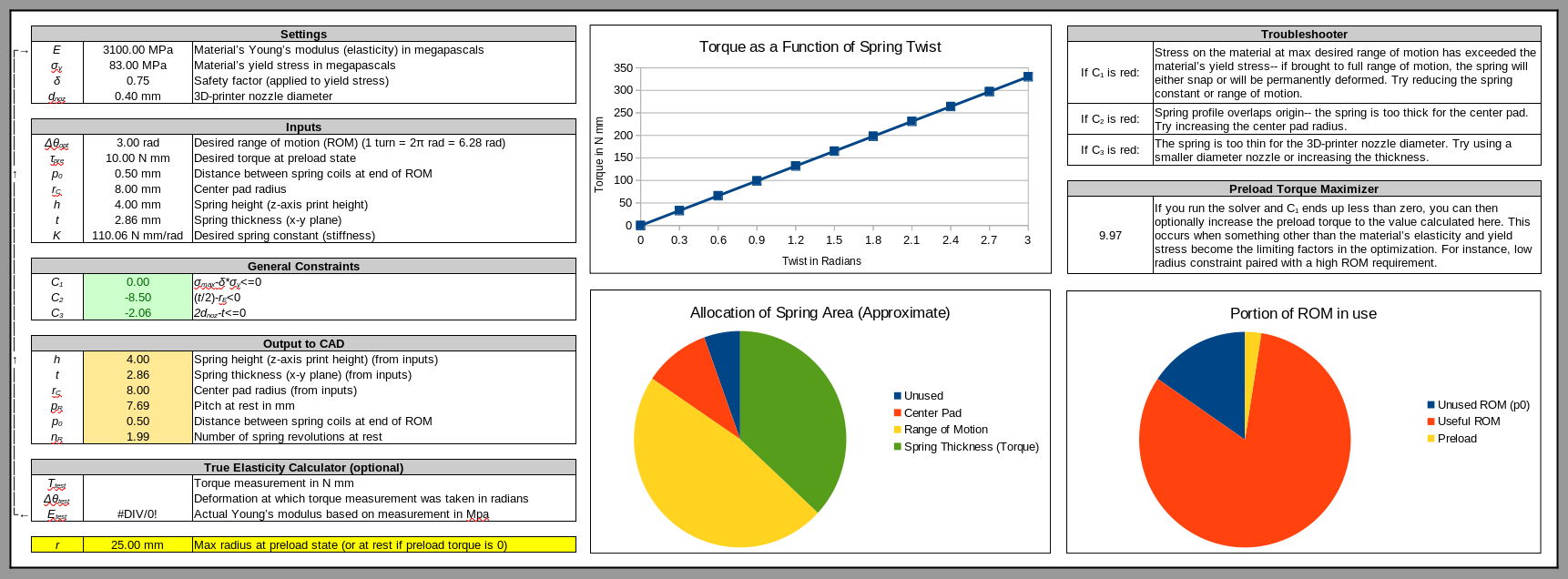
4. Nhập kết quả kiểm tra theo N mm vào ô D32 của bảng tính và lượng xoắn mà kết quả đó được ghi nhận theo radian vào ô D33.
5. Mô đun Young chính xác của vật liệu của bạn dựa trên kết quả này sẽ được tính trong ô D34. Bây giờ bạn có thể sao chép và dán nó vào ô D4, và lò xo sẽ được tính toán lại dựa trên mô đun thực tế.
6. Để đảm bảo nó hoạt động, hãy in lò xo vừa được tạo với cài đặt in tương tự như lò xo đầu tiên và kiểm tra lại mô-men xoắn. Bây giờ bạn sẽ nhận được kết quả mô-men xoắn chính xác được dự đoán bởi bảng tính (xem biểu đồ mô-men xoắn).
7. Đảm bảo đọc kỹ phần Hạn chế bên dưới.

Ứng suất chảy (σ_y):

Đây là mức ứng suất mà tại đó vật liệu sẽ rời khỏi “vùng đàn hồi” và bị biến dạng vĩnh viễn. Nó được sử dụng để tính toán ràng buộc C_1 trong bảng tính, sau đó được bộ giải sử dụng để đảm bảo độ đàn hồi đầy đủ của vật liệu (chịu sự chi phối của hệ số an toàn, xem bên dưới) được sử dụng. Nếu bạn muốn tối ưu hóa lò xo thực sự, bạn cần đảm bảo rằng bạn đang áp dụng gần bằng ứng suất chảy đầy đủ khi lò xo ở phạm vi chuyển động mong muốn tối đa của nó. Hiện tại tôi không có cách nào để xác định ứng suất chảy của vật liệu bằng thực nghiệm, vì vậy tôi chỉ sử dụng các số liệu do nhà sản xuất cung cấp.

Hệ số an toàn (δ):

Đây là hệ số được áp dụng cho ứng suất chảy để đảm bảo lò xo luôn nằm trong vùng đàn hồi mà nó có thể được sử dụng một cách đáng tin cậy. Tôi sử dụng hệ số an toàn là 0.75 vì đó là số liệu được các kỹ sư viết thuật toán được trích dẫn trong thư mục sử dụng.

Khoảng cách giữa các cuộn lò xo (p_0):

Đây là một tham số hữu ích vì hai lý do:

1. Trong bảng tính và trong tệp CAD, chúng ta đang xử lý một mô hình toán học hoàn hảo, nhưng lò xo thực tế được in ra sẽ có một số sai lệch về kích thước bất kể máy in của bạn tốt như thế nào. Ngay cả khi bạn muốn lò xo sử dụng hết không gian giữa các cuộn, bạn có lẽ nên sử dụng giá trị ít nhất là 0.05 hoặc 0.1 ở đây để tính đến điều này.
2. Khi lò xo bị biến dạng hoàn toàn cho đến khi nó chạm vào chính nó, sẽ có một lượng ma sát đáng kể gây ra sự thay đổi cách lò xo hoạt động. Ma sát này sẽ làm mất một phần năng lượng dự trữ của lò xo. Vì lý do này, bạn có thể muốn sử dụng một giá trị lớn hơn ở đây, ví dụ 0.3 hoặc 0.5, để đảm bảo điều này không xảy ra.

Một lưu ý về các mô hình CAD đi kèm:

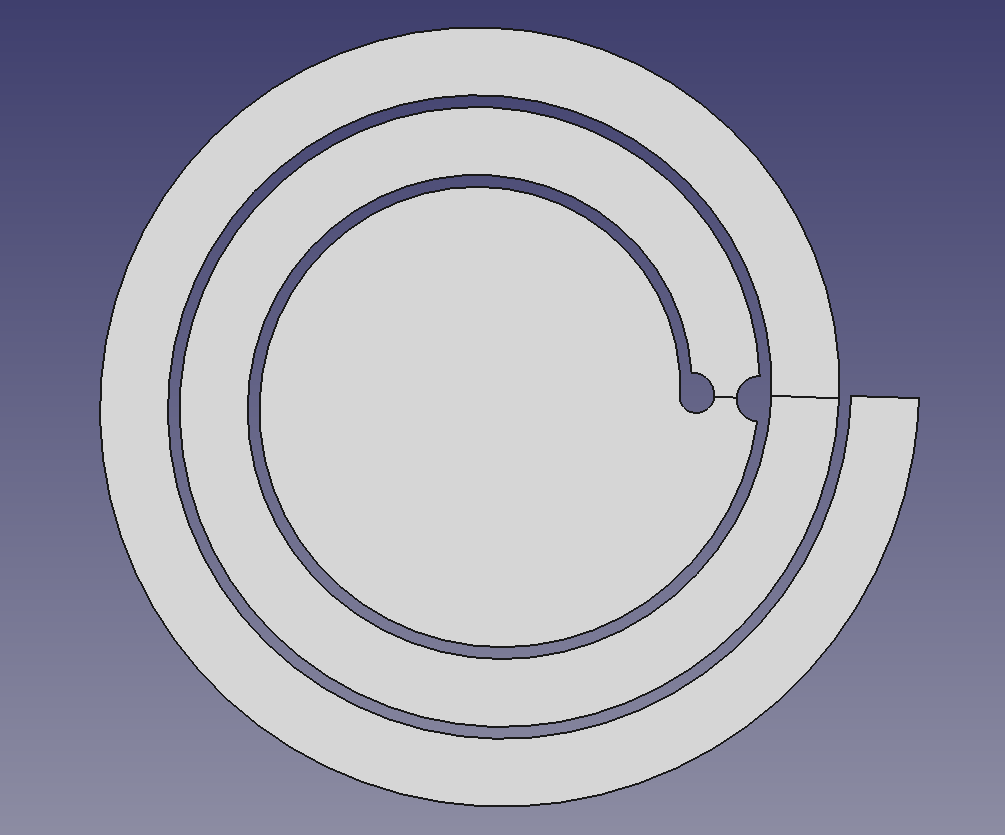
Trong các phiên bản trước, lò xo được hình thành bằng một hình tròn đơn giản cho miếng đệm trung tâm và bằng cách quay một hình chữ nhật quanh trục trung tâm để tạo ra lò xo. Vấn đề là: điều đó không tạo ra một xoắn ốc thực sự! Ngoài ra, xoắn ốc không bao giờ thoát ra một cách mượt mà khỏi miếng đệm trung tâm, luôn có một khoảng không gian chưa sử dụng ở đó làm mình bận tâm. Miếng đệm trung tâm mới thực chất được hình thành bởi một xoắn ốc-- một xoắn ốc có bước ren bằng bước ren của lò xo ở cuối phạm vi chuyển động của nó. Bằng cách đó, khi lò xo bị biến dạng hoàn toàn, ở mọi điểm, nó sẽ cách miếng đệm trung tâm một khoảng bằng khoảng cách với chính nó. Nói cách khác, khi lò xo bị biến dạng hoàn toàn đến điểm mà nó được thiết kế, tất cả không gian có sẵn ở trung tâm đều được miếng đệm trung tâm sử dụng hết. Ngoài ra, lò xo bây giờ được hình thành bởi một xoắn ốc thực sự và bằng cách quét một biên dạng lò xo vuông góc với xoắn ốc đó dọc theo chiều dài của nó. Điều này loại bỏ nhu cầu tính toán nhiều lần từ các phiên bản trước, vốn cần đặt biên dạng lò xo bên trong miếng đệm trung tâm để nối hai bộ phận.

Tham số r_C dùng để biểu thị bán kính của miếng đệm trung tâm này, và bây giờ nó biểu thị bán kính bên trong của xoắn ốc miếng đệm trung tâm. Vì vậy, nó về cơ bản vẫn kiểm soát cùng một thứ. Tham số r_P trước đây cần thiết để xác định khoảng cách từ gốc đến tâm của biên dạng lò xo, để nó bắt đầu bên trong miếng đệm trung tâm và thoát ra khỏi đó một cách mượt mà. Sau đó, r_E sẽ là điểm dọc theo xoắn ốc này nơi lò xo thực tế bắt đầu (điểm mà lò xo đã thoát hoàn toàn khỏi miếng đệm trung tâm). Điều này không còn cần thiết nữa, bây giờ biên dạng lò xo chỉ bắt đầu tại r_E. Số vòng quay n_P cũ được dùng để biểu thị số vòng quay từ biên dạng lò xo và đã được đổi thành n_R, số vòng quay của lò xo khi nghỉ vì không còn cần vòng quay thừa nữa.

Mô hình cũ:

Mô hình mới:

Mô hình mới ở biến dạng tối đa (phiên bản thử nghiệm):

Cách tối ưu hóa:

Về lý thuyết, bạn có thể sử dụng bảng tính này để tối ưu hóa lò xo theo nhiều cách khác nhau, nhưng đây là hướng dẫn từng bước cho những gì có lẽ sẽ là hình thức tối ưu hóa phổ biến nhất, đó là tối đa hóa hằng số lò xo (độ cứng):

1. Tải xuống Libreoffice Calc và đảm bảo bạn đã cài đặt tiện ích mở rộng NLP Solver của Sun Microsystems.
2. Mở bảng tính và nhập độ đàn hồi và ứng suất chảy của vật liệu của bạn từ bảng dữ liệu filament (hoặc từ phép đo của riêng bạn).
3. Nhập các giá trị cho tất cả các trường dưới “Inputs” ngoại trừ t và K.
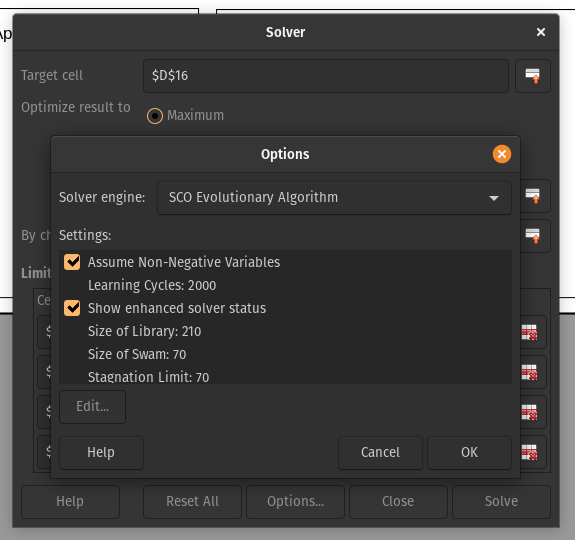
4. Vào tab “Tools”, và nhấp vào “Solver”. Trong hộp hiện ra, nhấp vào “Options” ở dưới cùng. Bên dưới “Solver engine”, chọn “SCO Evolutionary Algorithm”. Đánh dấu vào ô “Assume non-negative variables”. Nhấp OK để thoát tùy chọn.
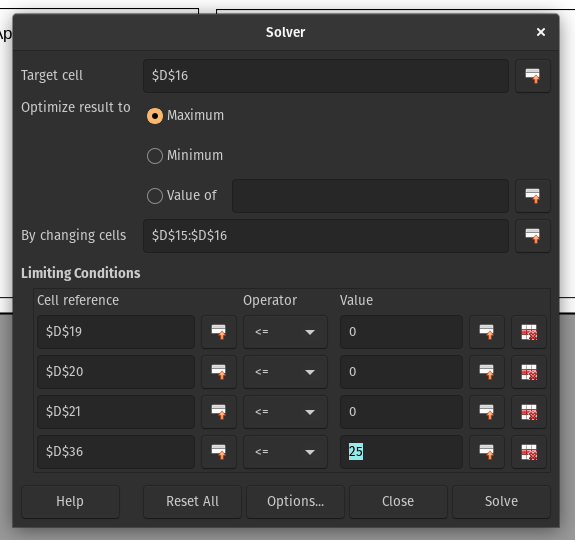
5. Đặt “Target Cell” thành giá trị K trong bảng tính (ô D16) và chọn “maximum”. Lưu ý: các ô của bạn có thể đã có tên như “solver_opt” thay vì “D16”. Đây là vì bộ giải lưu các cài đặt này. Vào “manage names” để thay đổi chúng.
6. Đặt “by changing cells” thành các ô D15-D16 (t và K). Việc tối đa hóa K bằng cách coi K là một biến số có thể là lạ, nhưng trong trường hợp này thì nó hoạt động.
7. Bây giờ là lúc để đưa vào các ràng buộc - bên dưới “Limiting Conditions”, đặt D19-D21 vào cột “cell reference” (từng cái một). đặt các toán tử thành “<=” và các giá trị thành 0.
8. Ràng buộc tùy chọn - Bạn gần như chắc chắn sẽ muốn giữ bán kính của lò xo dưới một kích thước nhất định. Đối với điều này, hãy sử dụng ô D36. Tôi cũng thích đặt ràng buộc để giữ độ dày của tôi nhỏ hơn hoặc bằng chiều cao của tôi, để lò xo dễ dàng giữ trong mặt phẳng của nó hơn.
9. Bây giờ hãy nhấn giải và xem nó chạy qua hàng nghìn ứng viên trước khi hội tụ về kết quả tốt nhất! Sau đó nhấp vào “OK” và “Keep result” nếu nó hoạt động. Nếu nó không hoạt động (nó sẽ báo “no solution found”) hãy thử nới lỏng một trong các ràng buộc. Ví dụ, có thể bạn đã đặt phạm vi chuyển động quá cao đến mức nó không thể tạo ra lò xo nhỏ như bạn mong muốn.

Hạn chế:

1. Công cụ này giả định rằng bán kính của lò xo sẽ được phép giảm tự nhiên khi lò xo bị biến dạng. Nếu đầu ngoài của lò xo được giữ cố định vào một vật thể cố định (như trong trường hợp nhiều lò xo xoắn 3D được in mà tôi đã thấy), thì công cụ này sẽ hoàn toàn vô dụng.
2. Công cụ này cũng giả định rằng “bản lề” của lò xo (phần lò xo kết nối với miếng đệm trung tâm) di chuyển tự do khi lò xo bị biến dạng, điều này rõ ràng không phải là trường hợp thực tế. Trong trường hợp lò xo rất mỏng, điều này không đáng kể, tuy nhiên, trong trường hợp lò xo dày vừa phải, điều này trở thành một vấn đề vì nhiều lý do. Nếu bạn muốn tạo ra một lò xo được tối ưu hóa, chính xác, hãy thử phiên bản CAD “bản lề linh hoạt” thử nghiệm.

Thư mục:

Bài báo này giải thích cách nhiệt độ và tốc độ in làm thay đổi các đặc tính vật liệu của vật thể in 3D. Đây là nơi tôi lấy các số liệu ban đầu về mô đun Young và ứng suất chảy:

Hsueh, Ming-Hsien & Lai, Chao-Jung & Wang, Shi-Hao & Zeng, Yu-Shan & Hsieh, Chia & Pan, Chieh-Yu & Huang, Wen-Chen. (2021). Effect of Printing Parameters on the Thermal and Mechanical Properties of 3D-Printed PLA and PETG, Using Fused Deposition Modeling. Polymers. 13. 1758. 10.3390/polym13111758.

https://www.researchgate.net/publication/351925060_Effect_of_Printing_Parameters_on_the_Thermal_and_Mechanical_Properties_of_3D-Printed_PLA_and_PETG_Using_Fused_Deposition_Modeling

Đây là một bài báo về một thuật toán tối ưu hóa khác cho lò xo xoắn 3D được in. Tôi đã cố gắng làm cho nó hoạt động trong bảng tính một lúc trước khi bỏ cuộc và quyết định tạo ra thuật toán của riêng mình từ đầu. Tôi đã sử dụng một vài thứ từ bài báo này, bao gồm cả ràng buộc C_1 của tôi. Tôi chủ yếu sử dụng cùng thuật ngữ từ bài báo này:

Scarcia, Umberto & Berselli, Giovanni & Melchiorri, Claudio & Ghinelli, Manuele & Palli, Gianluca. (2016). Optimal Design of 3D Printed Spiral Torsion Springs. V002T03A020. 10.1115/SMASIS2016-9218.

https://www.researchgate.net/publication/311169135_Optimal_Design_of_3D_Printed_Spiral_Torsion_Springs

Tôi cũng đã sử dụng một số phương trình từ omnicalculator và hưởng lợi rất nhiều từ lời giải thích về xoắn ốc Archimedean của nó.

Xin cảm ơn Symbolab rất nhiều vì đã giúp tôi kiểm tra lại đại số của mình.

Nhật ký thay đổi:

10/7/2025: Đã sửa vấn đề này với mô hình không khớp nối