Bảng analemma cong cho đồng hồ nắng heliochronometer

Tóm tắt Chỉ cần thay thế phần analemma đĩa phẳng gốc của bạn bằng mô hình đĩa cong này để cải thiện hiệu suất & tính thẩm mỹ của đồng hồ mặt trời heliochronometer hiện có của bạn. Xin lưu ý rằng thiết kế này chỉ tương thích với các đồng hồ heliochronometer ở bán cầu bắc. Đối với thiết kế analemma đĩa cong ở bán cầu nam, vui lòng tham khảo bản in này: Thiết kế analemma mới này tương thích với tất cả các mô hình đồng hồ heliochronometer gốc ở bán cầu bắc từ các F3D sau đây, vì vậy bạn sẽ không cần phải in lại bất kỳ bộ phận thay thế nào: - Đồng hồ mặt trời Heliochronometer Gard Derivative của yba2cuo3 | Tải mô hình STL miễn phí | F3D.com

• Heliochronometer - Đồng hồ mặt trời chính xác nhất thế giới của yba2cuo3 | Tải mô hình STL miễn phí | F3D.com
• Heliochronometer (phiên bản 2) - Đồng hồ mặt trời chính xác nhất thế giới của yba2cuo3 | Tải mô hình STL miễn phí | F3D.com Hiểu cách thiết kế một analemma là rất quan trọng cho việc xây dựng thành công và hoạt động chính xác của một đồng hồ mặt trời heliochronometer. Thiết kế này được lấy cảm hứng từ một thiết kế đồng hồ mặt trời Pháp cuối thế kỷ 19 có tên gọi “Radiguet” mà đã tích hợp một đĩa analemma cong (xem bên dưới). Bạn có thể tạo ra analemma đĩa phẳng hoặc cong của riêng mình theo hướng dẫn có trong bản in này, bao gồm tất cả các script Python để vẽ chúng trong Blender để xuất vào công cụ CAD yêu thích của bạn! Cập nhật (11-29-2024): - Thiết kế cải tiến để đơn giản hóa việc in, bao gồm đường cong analemma rõ ràng hơn & văn bản; - Thêm một thiết kế Nodus có thể điều chỉnh độ nghiêng được gắn trên một cánh tay thẳng đứng cong để Bù Đắp Độ Cao Mặt Trời trong suốt cả năm. Những thay đổi này cho phép một bóng sắc nét hơn được chiếu lên bề mặt Analemma, đặc biệt là ở các độ cao cực trị. Nếu bạn chưa có một đồng hồ heliocron và muốn tải xuống một thiết kế, hoặc bạn muốn có thêm thông tin về đồng hồ heliocron nói chung; tức là lịch sử, lý thuyết hoạt động, thiết kế, cách căn chỉnh và sử dụng, v.v. hãy tham khảo tài liệu in hữu ích này: Heliochronometer - Đồng hồ nắng chính xác nhất thế giới của yba2cuo3 | Tải mô hình STL miễn phí | F3D.com ### Cài đặt In - Thương hiệu máy in: Prusa
• Mẫu: i3 MK2S
• Hỗ trợ: Có
• Độ phân giải: 0.15mm hoặc 0.10mm
• Độ đầy: 20%
• Brim: Có - 10 đến 15mm
• Thương hiệu vật liệu in: Không quan trọng
• Chất liệu vật liệu in: ABS hoặc PLA
• Màu sắc vật liệu in: Không quan trọng
• Ghi chú đặc biệt: - In trong một hộp kín để có kết quả tốt nhất. ### Xây dựng Chỉ cần thay thế phần cánh tay thẳng đứng của đĩa analemma phẳng gốc của bạn bằng mô hình đĩa cong được cung cấp trong tài liệu in này. Điền vào khu vực bị lún bằng một chất làm đầy khắc như Markal B Paintstik Paint Pencil sau đó lau sạch phần thừa bằng một miếng vải khô, tiếp theo là một chút Isopropyl Alcohol để loại bỏ bất kỳ “vết bẩn” nào trên bề mặt chính. Ưu điểm: Đơn giản & Hiệu quả. Nhược điểm: Bừa bộn & không bền bỉ khi ở ngoài trời. Xem bài viết này để giải thích về quy trình: Ghi nhãn các bộ phận của bạn bằng chất làm đầy khắc Một tùy chọn khác là sơn khu vực bị lõm rồi chà sạch sơn thừa từ bề mặt chính. Ưu điểm: Bền. Nhược điểm: Bừa bộn & tốn công sức. Thật không may, điều này có thể làm mất một số chi tiết tinh xảo do ma sát cơ học nếu bạn không cẩn thận. Cụm Nodus Có Thể Điều Chỉnh Góc Tham khảo Hướng Dẫn Lắp Ráp Nodus Cong Có Thể Điều Chỉnh Góc trong phần tệp. ### Thiết Kế Bảng Analemma cho Đồng Hồ Thời Gian Mặt Trời Phương Trình Thời Gian (EoT) mô tả sự khác biệt giữa thời gian mặt trời; (được đo bằng đồng hồ mặt trời), và thời gian trung bình; (là thời gian mà một chiếc đồng hồ sẽ hiển thị). Sự khác biệt này dao động từ khoảng -14 phút vào đầu tháng Hai đến +16 phút vào đầu tháng Mười Một. #### Phương Trình Thời Gian và Hình Học Analemma Analemma phản ánh hai yếu tố trong chuyển động rõ ràng của mặt trời: - Quỹ đạo hình elip của Trái Đất: Điều này khiến mặt trời di chuyển nhanh hơn hoặc chậm hơn ở các điểm khác nhau trong quỹ đạo;
• Góc nghiêng trục của Trái Đất: Điều này khiến mặt trời xuất hiện cao hơn hoặc thấp hơn trên bầu trời vào những thời điểm khác nhau trong năm. Hai yếu tố này kết hợp tạo ra hình dạng số tám của analemma; điều này là kết quả của sự khác biệt giữa thời gian mặt trời và thời gian trung bình khi độ nghiêng của mặt trời (chiều cao so với đường chân trời) thay đổi trong suốt một năm mặt trời. Hình 1: Phương Trình Thời Gian so với Độ Nghiêng Mặt Trời (bán cầu bắc) #### Tỷ Lệ và Vẽ Analemma trên Bề Mặt Phẳng Chúng ta sẽ định nghĩa Phương Trình Thời Gian như sau; H = A – M trong đó; H = là Phương Trình Thời Gian (tính bằng phút, nhưng cần được chuyển đổi thành độ, hoặc góc giờ; tức là 15 độ = 60 phút); M = là Thời Gian Trung Bình, thời gian mà đồng hồ của chúng ta chạy; A = là Thời Gian mặt trời (rõ ràng). Thời gian dựa trên chuyển động thực tế của mặt trời của chúng ta & được hiển thị bởi một đồng hồ mặt trời không được hiệu chỉnh. Lưu ý rằng phương trình này ngược lại với một đồ thị analemma bình thường. Lý do là để phù hợp với việc chiếu/đường dẫn của 'vết nắng' lên tấm dọc của đồng hồ mặt trời từ nodus. ##### Tỉ lệ Chúng ta cần điều chỉnh tỉ lệ của đồ thị analemma để nó hoạt động với một đồng hồ mặt trời cụ thể. Việc điều chỉnh tỉ lệ là cần thiết để các kích thước của đồ thị analemma khớp với hình học vật lý của đồng hồ mặt trời mà nó được thiết kế cho; tức là kích thước của tấm đồng hồ, khoảng cách của gnome hoặc nodus từ tấm analemma, chiều cao của gnome hoặc nodus, v.v. Để làm điều này, chúng ta sử dụng dữ liệu EoT và độ nghiêng trung bình trong các năm 2000 đến 2047; tức là tham khảo earth_declination_eot.csv, và vẽ lại đường cong analemma để tính đến các tham số mà thiết kế đồng hồ mặt trời của bạn đặt ra. Nếu chúng ta muốn vẽ analemma của mình trên một tấm phẳng, thì chỉ cần chiếu đường cong lên một bề mặt 2D bằng cách sử dụng hình học đơn giản; tức là (tham khảo Hình 2); D = B ∙ tanδ E = B ∙ tanH Trong đó: δ = độ nghiêng của mặt trời; E = khoảng cách ngang từ đường kinh tuyến GT; D = khoảng cách dọc từ đường xích đạo GM; B = khoảng cách giữa nodus và các cánh tay analemma của alidade. Lưu ý: khoảng cách dọc từ lỗ nodus đến tấm đồng hồ tại G và khoảng cách dọc từ trung tâm tấm analemma tại M là giống nhau. Các biểu thức này dễ dàng được vẽ bằng cách sử dụng bảng tính, cùng với việc thêm các sự kiện thiên văn khác nhau làm dấu hiệu; tức là chí tuyến, điểm phân, tháng, v.v. Hình dưới đây làm nổi bật cách mà analemma sẽ được vẽ trên một tấm phẳng bằng cách sử dụng dữ liệu thu được từ các phương trình trên: Hình 2: Vẽ Analemma Đã Tỉ Lệ Trên Một Mặt Phẳng (bán cầu bắc) #### Vẽ Analemma Trên Một Bề Mặt Cong Các lỗi đọc liên quan đến việc sử dụng một tấm analemma phẳng trong một đồng hồ mặt trời phụ thuộc vào một số yếu tố; tức là - Lỗi Dự Đoán: Một tấm phẳng giả định một dự đoán đơn giản của analemma, có nghĩa là bóng đổ lên analemma không hoàn toàn theo đúng quỹ đạo mặt trời, đặc biệt là gần các cực của analemma (xung quanh các điểm chí). Sự khác biệt giữa vị trí bóng trên một tấm phẳng và thời gian mặt trời chính xác có thể gây ra một lỗi hệ thống;
• Độ Lớn Lỗi: - Tại các điểm phân: Lỗi do một tấm phẳng gây ra là tối thiểu vì bóng của mặt trời tương đối ổn định về phương diện độ nghiêng; - Tại các điểm chí (đông phân và hạ phân): Lỗi đạt mức tối đa. Độ lệch tối đa có thể là vài phút.
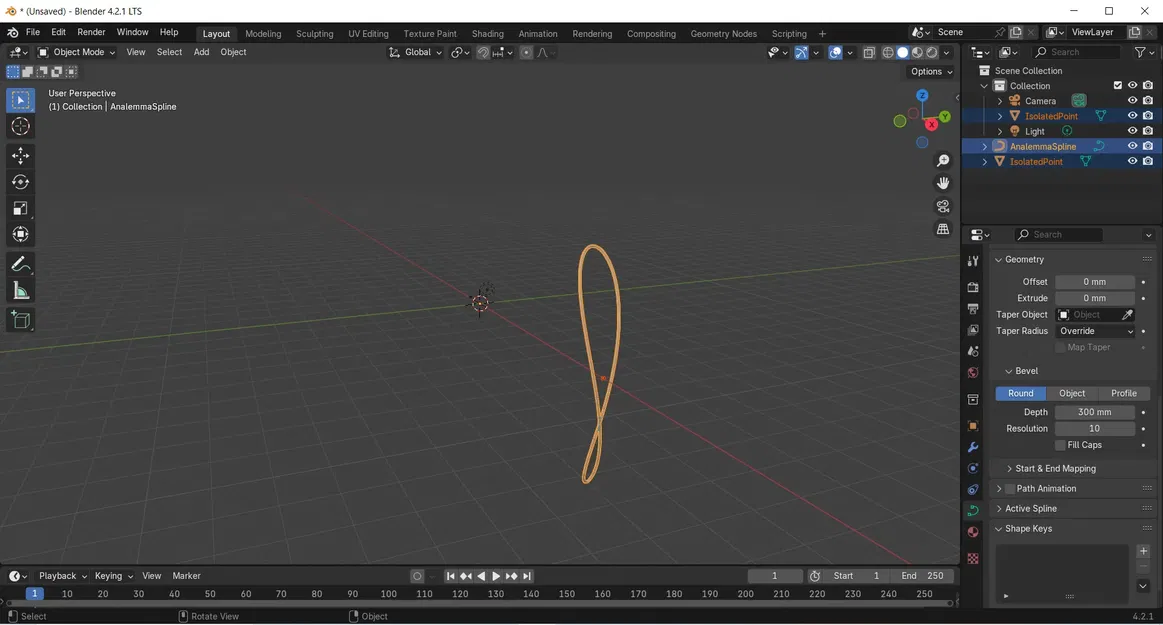
• Phụ Thuộc Vĩ Độ: Lỗi này không tồn tại trong các đồng hồ mặt trời ở xích đạo hoặc đồng hồ heliochronometer vì những loại đồng hồ mặt trời này có thể được điều chỉnh theo vĩ độ. Khi bạn nghiêng đồng hồ heliochronometer để phù hợp với vĩ độ của người dùng, nút sẽ được định hướng đến góc chính xác liên quan đến trục của trái đất. Sự điều chỉnh này sửa chữa các vấn đề liên quan đến vĩ độ về cách mà quỹ đạo của mặt trời xuất hiện trên bầu trời. Tính năng này giúp giảm đáng kể các lỗi liên quan đến vĩ độ vì hình học của thiết bị giờ đây được căn chỉnh để phản ánh độ cao và độ nghiêng mặt trời chính xác vào những thời điểm khác nhau trong năm. Giảm Thiểu Lỗi Sử Dụng Tấm Analemma Cong: Một analemma được vẽ trên một bề mặt cong sẽ theo sát quỹ đạo của mặt trời dọc theo một tấm đứng. Bằng cách tính đến Phương Trình Thời Gian và hình dạng của analemma, một tấm cong sẽ giảm thêm các lỗi đọc. - Lỗi Còn Lại: Với một tấm analemma cong được thiết kế đúng cách với độ nghiêng vĩ độ, lỗi còn lại trở nên tối thiểu, thường chỉ vài giây mỗi ngày bất kỳ lúc nào trong năm. Trường hợp ngoại lệ sẽ là các lỗi liên quan đến bất kỳ khuyết điểm nào trong xây dựng hoặc lắp ráp, hoặc bất kỳ giới hạn thiết kế và vật lý nào liên quan đến chính đồng hồ heliochronometer, giả sử tất nhiên rằng đồng hồ mặt trời được căn chỉnh và cân bằng hoàn hảo. Các yếu tố thiết kế ảnh hưởng đến lỗi: - Chiều cao Gnomon hoặc Nodus: Nếu gnomon hoặc nodus (phần tạo bóng) không tương thích đúng cách với một mặt phẳng hoặc mặt cong, lỗi sẽ tăng lên. ##### Vẽ các phương trình cho một bề mặt cong Để vẽ một analemma trên bề mặt cầu hoặc cong, chúng ta cần áp dụng một Hệ tọa độ Đề-các 3D; tức là X,Y,Z, theo cách sau: x(N) = B ∙ cos(δ(N)) ∙ cos(θ(N)) y(N) = B ∙ cos(δ(N)) ∙ sin(θ(N)) z(N) = B ∙ sin(δ(N)) trong đó; R = là bán kính của hình cầu vẽ; N = là ngày trong năm; tức là N = 0 đến 365; δ(N) = là độ nghiêng mặt trời tính bằng radian cho một ngày cụ thể; θ(N) = là Phương trình Thời gian (tính bằng phút, nhưng cần được chuyển đổi thành góc giờ; tức là 15 độ = 60 phút), Trong trường hợp của một đồng hồ heliocron, R giống như B được mô tả trong Hình 2 ở trên; tức là khoảng cách giữa nodus và các tấm dọc analemma trong thiết kế tấm phẳng. Trong thiết kế này, B = 80 (mm), nhưng nó có thể là bất kỳ kích thước nào khác miễn là các kích thước khác của đồng hồ heliocron được điều chỉnh phù hợp; tức là đường kính mặt số, chiều dài alidade, v.v. Các phương trình Đề-các ở trên đã được triển khai trong một bảng tính, với cả độ nghiêng & giá trị EoT là các biến đầu vào; tức là tham khảo earth_declination_eot.csv. Các giá trị tính toán kết quả sau đó được lưu vào một tệp csv khác; tức là earth_plot_analemma_3D.csv Dữ liệu trong CSV này phải được nhập theo định dạng sau (utf-8-sig phân cách bằng dấu phẩy) để các tập lệnh python có thể đọc dữ liệu một cách chính xác; tức là X0,Y0,Z0 X1,Y1,Z1 X2,Y2,Z2 ….. v.v. cho đến X(N), Y(N), Z(N) Để vẽ đường cong trong 3D, một tập lệnh python đã được viết để chạy dưới bảng điều khiển kịch bản Blender; tức là tham khảo earth_plot_analemma_3D.py Kịch bản đọc các giá trị từ tệp earth_plot_analemma_3D.csv và vẽ dữ liệu. Chỉ cần sao chép/dán kịch bản vào bảng điều khiển kịch bản của Blender. Nếu nó trả về bất kỳ lỗi nào, hãy kiểm tra các đường dẫn bạn đã chỉ định trong kịch bản có đúng không. Các đường dẫn sẽ cụ thể cho máy tính của bạn. Lưu ý quan trọng: Mỗi kịch bản cần được sửa đổi để bao gồm các đường dẫn tệp chính xác trên máy tính của bạn. Cũng hãy đảm bảo thay đổi phần mở rộng tên tệp từ .txt thành .py để nó có thể chạy dưới python. Khi đường cong được hiển thị trong Blender, bạn sẽ nhận thấy rằng các điểm dữ liệu được kết nối với nhau bằng các đường rất mỏng (splines). Nếu bạn không thấy bất kỳ đường cong nào, hãy phóng to ra. Các đối tượng được nhập vào Blender thường không được nhìn thấy do cài đặt phóng to mặc định. Bây giờ chúng ta cần gán thuộc tính vật lý cho nó và tăng độ dày của đường trước khi xuất nó dưới dạng mô hình CAD. - Đi đến biểu tượng đường cong màu xanh trong thanh bên; (góc dưới bên phải)
• Trong phần Hình học, bạn có thể sửa đổi Độ sâu Bevel và Độ phân giải theo nhu cầu. Một điểm khởi đầu tốt là độ sâu Bevel khoảng 300mm và độ phân giải là 10 để tạo cho đường cong một vẻ ngoài mịn màng. Đừng bị đánh lừa bởi kích thước độ sâu bevel. Blender hoạt động theo mét nên 300mm không phải là một bevel quá lớn. Khi bạn xuất đường cong, mọi thứ sẽ đến với tỷ lệ đúng. Analemma của bạn bây giờ nên trông như thế này trong Blender: - Khi bạn hài lòng với vẻ ngoài của đường cong analemma 3D, hãy đi đến Xuất sau đó .STL, (hoặc bất kỳ loại tệp CAD ưa thích nào của bạn). Hãy chắc chắn giữ tỷ lệ xuất là 1.00 (mặc định). Nếu bạn xuất sang STL, bạn có thể cần phải làm sạch và loại bỏ một số lỗi lỏng lẻo. Sử dụng một cái gì đó như Prusa slicer và chạy Sửa bằng Thuật toán Sửa chữa Windows, sau đó xuất lại sang STL ghi đè lên tệp cũ. Một dấu hiệu căn chỉnh luôn phải là một phần của biểu đồ analemma. Điều này giúp đơn giản hóa bất kỳ sự căn chỉnh vị trí nào với nodus và đảm bảo rằng cả analemma và nodus đều hoàn toàn được căn chỉnh trong các chiều X, Y và Z. Bất kỳ công cụ CAD nào mà bạn đưa đường cong analemma vào, dấu hiệu căn chỉnh này cần được đặt ở X=80, Y=0, Z=0 sao cho nó giữ nguyên tính nhất quán với thiết kế nodus của đồng hồ heliocronometer của bạn. Dấu hiệu đã được thêm thủ công vào tệp CSV analemma để ở 80 mm trong thiết kế này. Thêm Các Dấu Hiệu Bổ Sung vào Analemma Các dấu hiệu bổ sung có thể được thêm vào analemma để xác định các sự kiện như ngày đầu tiên của tháng, chí điểm và phân điểm, hoặc các sự kiện thiên văn khác. Ba kịch bản khác nhau đã được viết để người dùng có thể quyết định những dấu hiệu riêng biệt nào (nếu có) mà họ muốn chồng lên biểu đồ analemma 3D của mình; tức là: earth_plot_aphelion_perihelion_3d.py Dấu Hiệu Hình Vuông earth_plot_months_3D.py Dấu Hiệu Hình Tròn earth_plot_solstices_equinoxes_3D.py Dấu Hiệu Tetrahedron Lưu ý rằng các kịch bản trên dựa vào các tệp CSV riêng của chúng để nhập dữ liệu: tức là earth_plot_aphelion_perihelion_3d.csv earth_plot_months_3D.csv earth_plot_solstices_equinoxes_3D.csv Định dạng dữ liệu tệp đã lưu giống như tệp CSV analemma. Ngoài ra, các biểu đồ dấu hiệu đều có các dấu hiệu căn chỉnh riêng của chúng. Tất cả những điều này cần được chồng lên các dấu hiệu căn chỉnh analemma chính để đảm bảo tính nhất quán. >>>>> Tất cả các tệp .py và .csv được mô tả ở trên có sẵn để tải xuống trong phần tệp của tài liệu in này. <<<<< #### Chiếu Analemma 3D Đã Được Tỉ Lệ Lên Một Bảng Hình Cầu Nhập tệp STL Analemma 3D của bạn vào công cụ CAD yêu thích & định vị analemma sao cho dấu hiệu căn chỉnh của nó ở X=80, Y=0, Z=0. - Tạo một lớp vỏ hình cầu dày 5-10mm với bán kính bên trong là R; tức là 80mm trong ví dụ này. Đặt gốc của lớp vỏ tại 0,0,0. Bây giờ, analemma nên được nhúng & hoàn toàn căn chỉnh trên bề mặt bên trong của lớp vỏ. Tăng hoặc giảm nhẹ đường kính của lớp vỏ bên trong vào trong hoặc ra ngoài để có được sự nhúng đúng của đường cong Analemma vào bề mặt bên trong. Đừng di chuyển đường cong Analemma từ vị trí 80,0,0 trong quá trình này.
• Chọn một công cụ trích xuất Boolean trong công cụ CAD của bạn để đường cong trên lớp vỏ trông giống như một bản khắc; tức là nổi.
• Bạn có thể làm theo cùng một quy trình cho các điểm đánh dấu. Chỉ cần đảm bảo rằng tất cả các điểm đánh dấu căn chỉnh đều chồng lên nhau với điểm đánh dấu căn chỉnh analemma chính.
• Cắt bỏ lớp vỏ sao cho nó phù hợp với hình dạng bạn mong muốn. Thiết kế lớp vỏ sao cho nó có thể dễ dàng được in & gắn lên các khe gắn trên Alidade (cánh tay ngang) của đồng hồ heliocronometer.
• Nếu cần, điều chỉnh chiều cao của nodus sao cho lỗ nodus ở cùng chiều cao với điểm đánh dấu căn chỉnh của analemma của bạn. Nhớ rằng khoảng cách giữa lỗ nodus và bán kính bên trong của lớp vỏ analemma cần được giữ ở R. Cho tôi biết nếu bạn nhận thấy bất kỳ cải tiến nào trong đồng hồ heliocronometer của bạn về độ chính xác đọc! Nếu bạn nghĩ rằng đây là một thiết kế thú vị, đừng quên nhấn nút thích. Tôi hy vọng bạn thích xây dựng thiết kế này & cảm ơn sự hỗ trợ của bạn! ### Tài liệu tham khảo 1. Đồng hồ mặt trời - Cách xây dựng & Sử dụng, R. Newton Mayall & Margaret Mayall, Dover Publications Inc., 1994 2. Phương trình thời gian: Phương trình thời gian 3. Đồng hồ mặt trời Heliochronometer Gard Derivative của yba2cuo3 | Tải mô hình STL miễn phí | F3D.com 4. Heliochronometer - Đồng hồ mặt trời chính xác nhất thế giới của yba2cuo3 | Tải mô hình STL miễn phí | F3D.com 5. Heliochronometer (phiên bản 2) - Đồng hồ mặt trời chính xác nhất thế giới của yba2cuo3 | Tải mô hình STL miễn phí | F3D.com